
Ξέρω ότι διαίρεση λέγεται η πράξη με την οποία μοιράζουμε έναν αριθμό
σε τόσα ίσα μέρη, όσα μας λέει ένας άλλος αριθμός.
σε τόσα ίσα μέρη, όσα μας λέει ένας άλλος αριθμός.
- έναν δεκαδικό αριθμό με ακέραιο,
➜ κάνουμε τη διαίρεση σαν να είναι και οι δύο αριθμοί ακέραιοι,μέχρι να φτάσουμε στο τελευταίο ψηφίο του ακέραιου μέρους.
➜Μόλις φτάσουμε στο σημείο να κατεβάσουμε το πρώτο δεκαδικό ψηφίο, τότε βάζουμε υποδιαστολή στο πηλίκο και συνεχίζουμε κανονικά τη διαίρεση.
Για να διαιρέσουμε :
- έναν ακέραιο αριθμό με δεκαδικό,
➜ μεταφέρουμε την υποδιαστολή από τον διαιρέτη τόσα ψηφία πίσω, ώστε να γίνει ακέραιος αριθμός, γιατί διαίρεση με δεκαδικό διαιρέτη δε γίνεται.
Είναι σαν να πολλαπλασιάζεται με το 10,100 ή 1000, ανάλογα με το πόσα δεκαδικά ψηφία έχει.
➜Ο διαιρετέος πολλαπλασιάζεται και αυτός με το 10, 100 ή 1000, ανάλογα με ποιον αριθμό πολλαπλασιάστηκε ο διαιρέτης.
(προσθέτουμε μηδενικά, αν χρειάζεται )
Έτσι, η διαίρεση στην περίπτωση αυτή γίνεται διαίρεση ακεραίου με ακέραιο.
- δεκαδικό με δεκαδικό,
➜ πρέπει να μετατρέψουμε τον διαιρέτη από δεκαδικό αριθμό σε ακέραιο.
Γι' αυτό πολλαπλασιάζουμε τον διαιρέτη (ανάλογα με τα δεκαδικά ψηφία που έχει) επί 10 ή 100 ή 1000 κτλ.
Ταυτόχρονα πολλαπλασιάζουμε με τον ίδιο αριθμό και τον διαιρετέο.
μεταφέρουμε αντίστοιχα την υποδιαστολή μία ή δύο ή τρεις κτλ θέσεις προς τα δεξιά.
Αν δε μας φθάνουν τα δεκαδικά ψηφία που έχουμε, συμπληρώνουμε μηδενικά

 Γλώσσα
Γλώσσα 1η Ενότητα - Πάλι μαζί!
1η Ενότητα - Πάλι μαζί! Γ' Τάξη
Γ' Τάξη
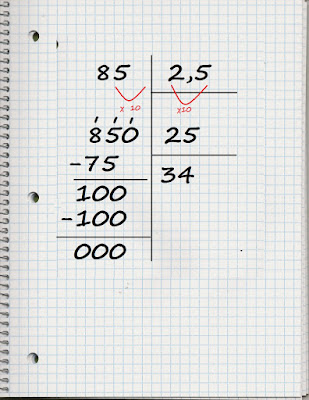









Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Το σχόλιό σου θα εμφανιστεί μόλις εγκριθεί