
Ένας σύνθετος αριθμός μπορεί να εκφραστεί και ως γινόμενο πρώτων αριθμών.
Για να μπορέσουμε να βρούμε το γινόμενο των πρώτων αριθμών ακολουθούμε μια διαδικασία που λέγεται παραγοντοποίηση.
Μπορούμε να αναλύσουμε ένα σύνθετο αριθμό σε γινόμενο πρώτων παραγόντων με δύο τρόπους:

- με δεντροδιαγράμματα
- με διαδοχικές διαιρέσεις
1 : με δεντροδιαγράμματα
➤ Έχουμε τον αριθμό 42.
➤Βρίσκουμε δύο αριθμούς που μας δίνουν γινόμενο 42.
➤Ο αριθμός 7 είναι πρώτος και δεν μπορεί να αναλυθεί.
➤Βρίσκουμε δύο αριθμούς που μας δίνουν γινόμενο 42.
➤Ο αριθμός 7 είναι πρώτος και δεν μπορεί να αναλυθεί.
➤Ο αριθμός 6 αναλύεται στους αριθμούς 2 και 3, που είναι και οι δύο πρώτοι αριθμοί.
➤Άρα, ο αριθμός 42 μπορεί να εκφραστεί ως γινόμενο πρώτων παραγόντων ως εξής :
42 = 7 x 2 x 3
Το αποτέλεσμα θα ήταν το ίδιο αν διαλέγαμε τους αριθμούς 2 και 21 :
42 = 2 x 3x 7
2 : με διαδοχικές διαιρέσεις
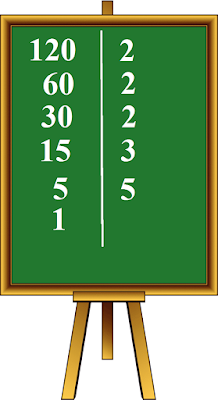
➤Έχουμε τον αριθμό 120.
➤Τον γράφουμε και τραβάμε μια κάθετη γραμμή στα δεξιά του.
➤Αρχίζουμε τη διαίρεση με το 2, που είναι ο μικρότερος πρώτος αριθμός.
➤Βρίσκουμε πηλίκο 60.
➤Διαιρούμε το 60 με το 2 και βρίσκουμε πηλίκο 30.
➤Διαιρούμε το 30 με το 2 και βρίσκουμε πηλίκο 15.
➤Διαιρούμε το 15 με το 3 και βρίσκουμε πηλίκο 5.
➤Διαιρούμε το 5 με το 5 και βρίσκουμε πηλίκο 1.
Εδώ τελειώνει η διαίρεση.
Το γινόμενο πρώτων παραγόντων του σύνθετου αριθμού
120 είναι : 120 = 2 x 2 x 2 x 3 x 5

 Γλώσσα
Γλώσσα 1η Ενότητα - Πάλι μαζί!
1η Ενότητα - Πάλι μαζί! Γ' Τάξη
Γ' Τάξη





Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Το σχόλιό σου θα εμφανιστεί μόλις εγκριθεί